Deep Neural Crossover 리뷰

원본 논문#

Deep Neural Crossover: A Multi-Parent Operator That Leverages Gene Correlations

GECCO ‘24: Proceedings of the Genetic and Evolutionary Computation Conference, 2024

요약#

Deep Neural Crossover(DNC)라는 신경망 방법을 사용한 crossover 방법을 소개 다른 crossover방법과 비교해서 최적해를 빠르게, 정확하게 찾을 수 있음

사전설명#

crossover를 설명하기 전에 먼저 유전 알고리즘(genetic algorithms)의 전반적인 내용을 알아둘 필요가 있음

유전(또는 진화) 알고리즘이란 생물체의 진화형태를 모방한 최적해 탐색 알고리즘으로, 개별의 적합도(최적화를 목표로 하는 값)을 계산 후 유전자 선택 후, 해당 유전자를 교차(crossover), 변이 등을 거침

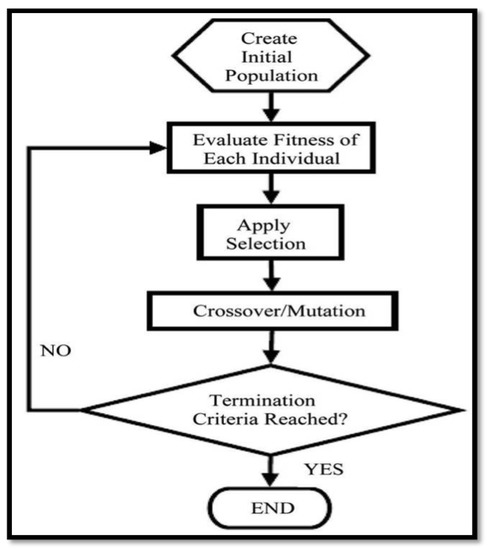
(유전 알고리즘의 순서도, 출처 : Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach)

교차는 one-point crossover, two-point crossover 등이 있음 (n번을 나눌건지에 따라 point 개수가 늘어난다고 생각하면 편함. 이후 일정확률에 따라 서로 유전자를 교차. (쉽게 말해서 데이터를 바꿈)) 그렇기 때문에 crossover를 잘 선택하는것이 중요하다고 할 수 있음.

(one-point crossover, 출처 : https://en.wikipedia.org/wiki/Crossover_(genetic_algorithm))

1. 도입부#

기존의 유전 알고리즘 교차 연산자들은 주로 부모의 유전자를 무작위로 선택하지만, DNC는 심층 강화 학습(Deep Reinforcement Learning, DRL)과 인코더-디코더(Encoder-Decoder) 구조를 활용하여 더 나은 유전자 선택을 학습함.

DRL을 통해 유전자를 선택하는 정책을 학습하며, 이 정책은 확률적이기 때문에 무작위성을 유지하면서도 결과적으로는 더 나은 적합도를 가진 유전자가 선택될 확률이 높아짐. 이 과정에서 장단기 메모리 (LSTM)가 사용되며, 부모의 유전체 정보를 잠재 메모리 상태로 인코딩하고, 디코더의 LSTM이 어텐션 기반의 포인팅 메커니즘(attention-based pointing mechanism)을 사용해 자손의 다음 유전자를 선택하는 분포를 생성할 수 있도록 함.

2. 상세설명#

Deep Neural Crossover#

DNC는 인코더와 디코더로 구성

인코더#

인코더는 LSTM 셀을 기반으로 하여 부모의 유전체 정보를 임베딩된 표현(embedded representation)으로 변환함. 각 유전자는 학습 가능한 잠재 벡터로 표현되며, 이 벡터는 부모 유전체의 임베딩된 상태로 변환이 됨. 두 부모의 유전 정보를 각각 처리하여 최종적으로 두 부모의 임베딩 표현을 결합한 2차원 벡터를 생성함.

디코더#

디코더 역시 LSTM 셀로 구성되며, 부모 유전체의 임베딩 표현을 입력으로 받아 자손의 유전체를 생성함. 여기서 디코더는 각 단계에서 포인터 네트워크의 메커니즘을 통해 부모의 유전체 중 어느 유전자를 선택할지 확률 분포를 생성함.

Reference vector#

참조 벡터는 포인터 네트워트가 자손의 다음 유전자를 선택할 때 사용할 수 있는 입력 데이터로, 임베딩 되기 전에 부모의 각 유전자 위치에서 변환된 벡터들이다.

Query vector#

쿼리 벡터는 포인터 네트워크에서 자손의 다음 유전자를 선택할 때 참조 벡터 중 어느 부모의 유전자를 선택할지 계산하는 데 사용됨. 쿼리 벡터는 디코더의 현재 상태와 연결되며, 이 벡터를 이용하여 포인터 네트워크는 어느 부모의 유전자를 선택할 확률을 계산함.

포인터 네트워크#

포인터 네트워크는 어텐션 메커니즘과 유사하지만, 어텐션 메커니즘에서의 softmax를 구하고 encoder에 합치는 것이 아니고 softmax 자체를 사용하는 모델

출력이 softmax 함수로 구성되어있기 때문에 이 네트워크는 특정 부모의 유전자를 선택하는 확률을 계산할 수 있으며, 가장 높은 확률을 가진 유전자를 선택할 수 있다.

강화학습 기반 유전자 선택#

DNC는 강화 학습을 사용하여 유전자 선택 과정에서의 정책을 최적화함. 강화학습의 보상은 생성된 자손의 적합도(fitness score)를 기반으로 하며, 자손의 적합도를 최대화하는 것이 목표로 설정함. 이를 위해 정책 그래디언트 방식인 REINFORCE 알고리즘을 사용해 학습을 진행하며, 몬테카를로(Monte Carlo) 샘플링을 통해 부모와 자손의 데이터를 학습에 활용

다중 부모 지원#

DNC는 2명의 부모뿐만 아니라 여러 명의 부모를 지원함. 다중 부모의 유전체를 임베딩된 상태로 변환하고, 포인팅 네트워크를 통해 여러 부모의 유전체 중 어느 유전자를 선택할지 결정할 수 있다.

사전 학습 적용 가능#

DNC는 기본적으로 교차 연산이 일반적인 유전 알고리즘보다 더 많은 시간과 연산을 소모하기 때문에, 이를 개선하기 위해 사전 학습 방법(Pre-Training)을 제안했다. 특정 문제 도메인에서 먼저 학습을 진행한 후, 동일한 도메인 내의 다른 문제를 해결할 때 이미 학습된 네트워크를 재사용함으로써 시간 소모를 줄이고 성능을 향상시킬 수 있다고 함.

3. 실험 결과#

모든 실험에서 1024개의 시퀀스로 구성된 미니 배치, 64개의 LSTM 셀을 사용하고 유전자는 64차원 공간에 임베드됨. 모델을 훈련하기 위해 adam, 10^−4의 학습률, 0.2의 입실론 그리드, 100개의 individuals, 6000 세대, 유전자 선택은 토너먼트 선택(𝑘 = 5), uniform 변이(확률 0.01 =>1%), 교차 확률은 0.5=>50%로 설정함.

Table 1: Graph Coloring (그래프 색칠 문제)#

그래프 색칠 문제는 주어진 그래프에서 인접한 두 정점이 같은 색을 가지지 않도록 하면서 최소한의 색을 사용해 그래프를 색칠하는 문제임. 이 실험에서는 DIMACS 데이터셋을 사용하여 여러 벤치마크 그래프를 대상으로 평가함. 각 실험에서 자손이 사용하는 색상의 수를 최소화하는 것이 목표

Table 1에서 제시된 수치는 각 알고리즘이 특정 문제에서 사용한 평균 색상의 수로, 값이 낮을수록 더 적은 색을 사용해 문제를 해결했음을 의미하며, 즉 더 나은 성능을 나타냄.

Table 2: Bin Packing Problem (이진 적재 문제)#

이진 적재 문제는 정해진 용량을 가진 여러 개의 상자에 물건을 최소한의 상자를 사용하여 효율적으로 담는 문제로, 각 상자에 물건이 넘치지 않도록 해야 하며, 목표는 사용된 상자의 수를 최소화하는 것임. 이 실험에서는 Schoenfield_Hard28 데이터셋을 사용하고, 각 알고리즘이 얼마나 적은 상자를 사용해 물건을 적재했는지 평가됨. 해당 테이블에서 제시된 수치는 적재 효율을 나타내며, 값이 클수록 상자를 적게 사용했음을 의미

또한 NeuroCrossOver(NeuroCrossover: An intelligent genetic locus selection scheme for genetic algorithm using reinforcement learning) 방법과 비교했을때(Table 3) 성능이 더 좋았으며, Figure 3은 각 세대에서 다른 교차 연산자가 최대 적합도에 미치는 영향을 시각화한 것으로, 다른 교차 연산자 대비 빠른 세대 안에서 더 적은 색을 사용할 수 있는 해를 찾음

Table 4는 세대별 시간 측정으로, DNC가 기존 알고리즘에 비해 더 높은 시간 비용을 발생시키긴 하지만, 사전 학습된 DNC-PT는 시간 비용을 크게 줄일 수 있음을 보여줌

결론#

DNC는 실험 데이터 셋의 결과를 통해 유전자 선택 과정에서 강화 학습을 통합하여 유전 알고리즘의 성능을 향상시킨다는 점을 강조함. 이 새로운 교차 연산자는 기존의 무작위적인 자손 생성 방식에서 벗어나, 심층 강화 학습을 통해 더 높은 적합도를 가진 자손을 선택할 수 있는 확률 분포를 학습함.

그리고 DNC는 유전자 간의 비선형 상관관계를 학습하여, 자손을 생성할 때 유용한 유전자를 더 많이 선택하는 방향으로 최적화가 가능함을 보임. 또한 DNC는 다중 부모 교차도 지원하여 성능을 더욱 향상시킬 수 있으며, 사전 학습 기법을 통해 실행 시간을 줄이는 동시에 성능도 개선할 수 있다는 것을 입증함.

사용방법#

저자들이 올린 코드를 사용할 수 있음.

1
from selection_ga import SelectionGA
2
from multiparent_wrapper import NeuralCrossoverWrapper
3
import numpy as np
4
import torch
5
import json
6
import os
7

8

9
def get_bin_packing_fitness(individual, fitness_dict, penalty=100):
10
    global item_weights, bin_capacity
11

12
    if tuple(individual) in fitness_dict:
13
        return fitness_dict[tuple(individual)]
14

15
    fitness = 0
16
    bin_capacities = np.zeros(n_items)
17
    legal_solution = True
18

19
    for item_index, bin_index in enumerate(individual):
20
        bin_capacities[bin_index] += item_weights[item_index]
21

22
        if bin_capacities[bin_index] > bin_capacity:
23
            legal_solution = False
24
            fitness -= penalty
25

26
    if legal_solution:
27
        utilized_bins = bin_capacities[bin_capacities > 0]
28
        fitness = ((bin_capacities / bin_capacity) ** 2).sum() / len(utilized_bins)
29

30
    fitness_dict[tuple(individual)] = fitness
31
    return fitness
32

33

34
PERMUTATION = False
35
datasets_json = json.load(open('./datasets/hard_parsed.json', 'r'))
36
PATH_TO_EXP = f'./experiments/bin_packing/DNC/'
37
dataset_name = 'BPP_14'
38
item_weights = np.array(datasets_json[dataset_name]['items'])
39
bin_capacity = datasets_json[dataset_name]['max_bin_weight']
40
n_items = len(item_weights)
41
n_parents = 2
42
print(dataset_name, n_items)
43

44
try:
45
    os.makedirs(os.path.join(PATH_TO_EXP, dataset_name))
46
except FileExistsError:
47
    pass
48

49
params_dict = {
50
    'n_generations': 6000,
51
    'population_size': 100,
52
    'crossover_prob': 0.5,
53
    'mutation_prob': 0.5,
54
    'ind_length': n_items,
55
    'save_every_n_generations': 5,
56
    'min_selection_val': 0,
57
    'max_selection_val': n_items - 1,
58
    'flip_mutation_prob': 0.1,
59
    'tournament_size': 5,
60
    'save_population_info': False,
61
    'save_fitness_info': False,
62
    'elitism': False,
63
    'n_parents': n_parents
64
}
65

66
torch.manual_seed(4242)
67
ncs = NeuralCrossoverWrapper(embedding_dim=64, sequence_length=n_items, num_embeddings=180 + 1,
68
                             running_mean_decay=0.95,
69
                             get_fitness_function=lambda ind: get_bin_packing_fitness(ind, ga_class.fitness_dict),
70
                             batch_size=2048, freeze_weights=True,
71
                             load_weights_path=None, learning_rate=1e-4,
72
                             epsilon_greedy=0.3, use_scheduler=False, use_device='cpu', n_parents=n_parents)
73
ga_class = SelectionGA(**params_dict, random_state=42)
74
ga_class.fit(PATH_TO_EXP, get_bin_packing_fitness, crossover_func=ncs.cross_pairs)

후기?#

유익했던 논문이며, selection 방법에도 선택하는데 있어서 선택 정책을 강화학습을 이용해서 풀수 있지 않을까 생각함. 또한 다양한 crossover(multi-point, extended box)에 대해서도 멀티 암 밴드 등을 적용해서 할 수 있는 논문이 나오지 않을까 기대함.